振荡电路
电子琴、音乐合成器等电子乐器奏出各种各样的声音。这种电子声音由振荡电路产生的低频信号合成生成。
另外,电波将声音等信号调制在高频信号上由天线发射出去,而成为这一电波基础的高频载波信号也由振荡电路产生。
并且,为了对音响设备和无线设备进行试验及调试,振荡电路也应用于各种各样的信号发生器中。
振荡电路就这样成为产生低频、高频电信号的重要电路。
这里,我们学习由正反馈产生振荡的机理,分析调谐式、哈特莱式、科耳皮兹式、晶体振荡、RC振荡电路等各种振荡电路的工作原理,并且,振荡频率的变化与稳定进行学习。
7.1
利用正反馈产生振荡7.1.1
产生交流信号的振荡电路振荡电路是即使不施加输入信号,只要将电源开关置于ON,在输出端也会产生低频或高频的交流信号的电路(参照图7.1)。
放大电路一旦增益提高或信号的频率变高,就由于Tr的内部反馈及感应而产生振荡。一旦电路振荡起来,即使输入为0也有信号输出,使得放大不能再进行。
振荡电路是控制电路的振荡状态以获得所需振荡频率和振荡电压的电路。
7.1.2
施加正反馈产生振荡图7.2表示产生振荡的正反馈的原理。振荡电路由Tr决定的放大电路和正反馈电路构成。
若对放大电路加上初始输入信号Ii,则它被放大成为输出信号Io出现在输出端。这一Io的一部分Iβ通过正反馈电路返回到输入端。这时,若初始输入信号和反馈信号为同相,则Ii和Iβ互相加强,Ii+Iβ再次被放大使输出信号增大。其中的一部分再次以同相的方式返回到输入。如此反复进行,就变为即使输入为0,但只要有反馈信号即可获得输出。这就是振荡状态(图7.4)。
输入信号和反馈信号变为同相的情况称为正反馈。另外,初始的输入信号为电源开关置ON的瞬间,在电路中产生的衰减振荡。即使正反馈反复地进行,但因为Tr的非线性及饱和特性,输出信号也不超过某个值,Tr不至于被毁坏。
7.1.3
初始的输入信号是什么已学过振荡是由正反馈引起的。那么,输入信号是如何施加的呢?
在收音机和音响等中,当电源开关置于ON的瞬间,从扬声器中可以听到杂音。这是由于在电源施加瞬间,由冲击所引起的电信号被放大的结果。振荡电路的初始输入信号就是在这一瞬间产生的杂音。这个杂音是由于电路中的线圈和电容器的作用引起的。这里,对线圈和电容器的作用做详细的分析。
图7.5(a)是LC并联谐振电路。若对这个电路加上电压,则电容器被充电。一旦充电完毕,电容器中贮存的电能就通过线圈进行放电。这时,线圈中储存磁能。于是,这次是从线圈向电容器释放能量,电容器中储存进电能。如果能量没有损失,电容器的充电和放电反复进行,电流在C与L之间来来去去不断地流通。但是,由于线圈的电阻等原因能量衰减,电流减小变为衰减振荡。
这就成为振荡电路的输入信号。
7.1.4
振荡电路的振荡条件如图7.6所示,振荡电路由放大电路和正反馈电路构成。让我们根据该图对振荡电路的振荡条件进行分析。
电源开关置于ON,则产生衰减振荡Ii,它被放大Ai倍呈现为输出电流Io。然后,Io的一部分βIo通过正反馈电路返回到输入。这时Ii和Iβ因同相互相增强,以Ii+Iβ输入使Io增大。它的一部分再次被正反馈,振荡开始。
因为初始的输入电流Ii为衰减振荡,所以如果反馈电流Iβ不满足
I
β≥Ii则输出电流Io也衰减。这时放大电路和反馈电路的闭环增益Aiβ变为
A
iβ≥1上式表示振荡电路的振荡条件。
在振荡的初期,由于Iβ比Ii小,环路增益变为
![]()
![]()
产生增幅振荡。输出电流不断增加,当Iβ变得与Ii相等时,有
![]()
振荡成为等幅振荡。
即使正反馈反复进行,但输出电流没有增加到毁坏Tr的程度的原因是由于放大电路的非线性和饱和特性,使Io达到饱和。
7.2
变压器耦合调谐式振荡电路7.2.1
用振荡变压器实现正反馈共发射极放大电路的输入与输出为反相即有180○的相位差。为了在输入端加上正反馈,必须使输出信号的相位超前180○(滞后180○结果也一样)再返回到输入端。
振荡变压器在同一个磁芯上缠绕着初级线圈和次级线圈,根据互相感应,缠绕方向以相对于施加在初级端的电压,次级端的电压有180○的相位差为准。
图7.7(b)L1和L2中的·标记称为同名端,表示变压器线圈的极性。在图示情况下,L1和L2的·标记相反的标于图中,说明初级端和次级端存在180○的相位差。
线圈的Q值对振荡电路的稳定性具有很大的影响。另外,为使输出与输入耦合,也必须进行阻抗匹配。为此,引出中端引线以提高Q值,同时取得匹配。
7.2.2
三种调谐式振荡电路调谐式振荡电路中由振荡变压器的线圈与电容器连接构成调谐电路。在这个调谐电路中,只有调谐频率fr的信号放大Q倍产生振荡。振荡频率由调谐电路的L、C的值决定。
根据是在晶体三极管的C、B、E三个电极中的哪个电极进行调谐的,分别有集电极调谐式振荡电路、基极调谐式振荡电路和发射极调谐式振荡电路。基极调谐式常被用于超外差式接收机中的本地振荡电路中(图7.8)。
7.2.3
振荡频率有多少HZ图7.9是集电极调谐式振荡电路。它由使用2SC1815的放大电路,C1、L1构成的调谐电路以及L1、L2、C2构成的正反馈电路三块组成。一旦电源开关置于ON加上直流电压,则最初由C1和L1产生衰减振荡,在L2上感应出反相的反馈电压。它通过C2加到基极,开始振荡。振荡频率基本由C1和L1决定,可按下式求得:
![]()
7.3
哈特莱式和科耳皮兹式振荡电路7.3.1
利用L和C加上正反馈图7.10(a)称为哈特莱式,图(b)称为科耳皮兹式振荡电路,用线圈和电容器施加正反馈产生振荡。两个电路都将输出电压Vo在L和C上分割为V和Vβ这时,若使Vo和Vβ变得相位相反(相位差180○),则加上正反馈产生振荡。
科耳皮兹式振荡电路与哈特莱式相比,只是将L与C调换,是完全对偶的电路。另外,工作原理上也因为是由L和C来进行分压而相同。
7.3.2
哈特莱式振荡将图7.10(a)重画为易于理解的形式就如图7.11所示。在该电路中一接通电源,LC电路就产生衰减振荡,形成初始输入信号。它被Tr放大成为输出信号vo。
共发射极放大电路的输入电压相位和输出电压的相位为反相(180○)。于是vo被L1和C分压,得到与vo反相的反馈电压vβ,若将其再输入基极,则电路就加上正反馈而产生振荡。
对照图7.12的矢量图,让我们对由电压分压产生的正反馈的情况作更详细的分析。
若考虑以流过C和L1的反馈电流Iβ为基准,则C上的端电压V滞后90○,而L1上的端电压Vβ超前90○,如下式所示:
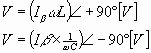
由上式和矢量图可见,V和Vβ的相位差为180○。这里若选择L1和C的值使之满足1/(ωC),则有V>Vβ
输出电压Vo变为Vo=Vβ+V,由下式表示:
![]()
V
o和Vβ的相位差为180○。如此计算求得反馈电压Vβ。哈特莱式的振荡频率可由下式决定:
![]()
只是,M为当L1和L2缠绕在同一个磁芯的情况下的互感系数,若无互感,则为0。另外,这个电路的起振条件为(参照图7.13)
h
fe≥L1/L2 (hfe:Tr的交流电流放大系数)7.3.3
科耳皮兹式振荡图7.10(b)是科耳兹式振荡电路的原理图。这个电路与哈特莱式很想像。重画该电路如图7.14所示,分析这一电路的振荡情况。
在科耳皮兹电路被接通的瞬间,LC电路中产生衰减振荡,晶体三极管的基极加上初始输入电压,集电极呈现输出电压vo。在共发射极Tr放大电路中,输入电压与输出电压的相位差为180○。
这一输出电压vo被由L和C组成的反馈电路进行分压,反馈电压vβ反馈回基极。如果vβ与初始输入电压同相,则电路中加上正反馈产生振荡。
图7.15是科耳皮兹式振荡电路中各部分的电压和电流的矢量图。同样这里也利用矢量图对正反馈的情况进行分析。
现在,若以反馈电流Iβ作为参考的基准,则L的端电压V超前90○。另外,C1的端电压Vβ滞后90○,V和Vβ的相位差变为180○如下式所示:
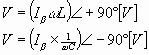
这里,若选择L和C1的值使得,则V和Vβ的大小满足V>Vβ。另外Vo由Vo=V+Vβ求得,表示为
![]()
V
o和Vβ 的相位差变为180○即加上正反馈。图7.16是科耳皮兹式振荡电路的实例。7.4
频率稳定的晶体振荡电路7.4.1
产生谐振现象的石英晶体图7.17所示的石英晶体是由从石英结晶上切割出的石英薄片及涂敷在其两面的电极板构成的。一旦对其施加电压就产生机械的应变,反之,对其施加压力就产生电压。这一现象称为压电效应(参照图7.17(c))。
若对石英晶体施加交流,则在某一频率上产生谐振,流过很大的电流。由石英晶片的厚度及与结晶轴的角度决定石英晶体的固有频率,当它与外加交流的频率变得一致时,谐振发生。这与LC电路的谐振现象相同。
7.4.2
使用石英晶体代替线圈研究石英晶体的电气特性可知,它具有与图7.18(a)所示的等效电路相同的作用。图7.18(b)为石英晶体的电抗频率特性。在石英晶体的固有频率fo产生由Lo、Co、ro决定的串联谐振,在fo'产生由C和Lo、Co、ro决定的并联谐振。
在fo<f<fo'的极狭小范围内,它呈现感应性作为线圈工作。而在其它频率作为电容工作。Q值非常高且由于受温度影响小,在LC振荡电路中若代替线圈使用,则可获得稳定的振荡频率。利用石英晶体的振荡电路称为皮尔斯振荡电路。
7.4.3
使用石英晶体的皮尔斯电路图7.19(a)所示为石英晶体使用于哈特莱振荡器的电路,称为皮尔斯BE电路,集电极调谐电路呈现感性而产生振荡。图(b)所示为使用于考毕兹振荡器的电路,称为皮尔斯CB电路。调谐电路呈现容性。
晶体振荡电路的振荡频率为石英晶体的固有振动频率。图7.20是皮尔斯BE电路的实例。
7.5
利用R和C实现正反馈的RC振荡电路7.5.1
利用R和C产生振荡在LC振荡电路中,若要产生低频的振荡,则因为必须使用又大又重的大容量的电容器及线圈,故不实用。
为此,使用仅由R和C实现正反馈的RC振荡电路产生低频振荡。RC振荡电路中有用移相电路实现正反馈的移相式电路和由于两级放大电路的输出信号与初级输入信号的相位差为0而在输入端呈现正反馈的桥式电路等。
7.5.2
移相180○实现正反馈的移相式移相式振荡电路由如图7.21所示的放大电路和移相电路构成。放大电路的输出电流用三级移相电路移相180○,在输入端形成正反馈。每一级的相位差为60○。相位以超前的形式实现正反馈的电路称为HP导前移相式(高通),而以滞后形式实现的称为LP滞后移相式(低通)(图7.22)。
图7.22是移相式振荡电路的原理图。仅将HP式移相电路中的一级电路在图7.24中画出,用以分析相位的移动情况。
若以Vo为参考基准,则IR为同相,IC超前90○。若选择R和C,满足![]() ,则IC比IO超前60○。因此若将这样的电路三级级联,则相位超前180○,对放大电路实现正反馈而产生振荡。
,则IC比IO超前60○。因此若将这样的电路三级级联,则相位超前180○,对放大电路实现正反馈而产生振荡。
如果将HP型中的R和C互换,就形成LP型电路。如IC/IR变为![]() ,则IR比IO滞后60○,三级电路级联移相180○。
,则IR比IO滞后60○,三级电路级联移相180○。
图7.23是移相式振荡电路的实例。RB、RE、R用于给晶体三极管加上偏置。CE是旁路电容。这个电路为HP型,移相电路由3个4.7kΩ的电阻和3个0.022μF的电容构成。
7.5.3
桥式振荡电路放大电路的输入信号和输出信号反相,具有180○的相位差。若进行两级放大则可获得与初级输入信号同相的输出信号。
在桥式电路中,第2级放大电路的输出信号由RC反馈电路保持原相位不变,返回到初级的输入端形成正反馈。由于放大电路的增益增大,所以加上负反馈使放大稳定化(参照图7.25)。
图7.26所示是桥式振荡电路,由Tr1和Tr2的两级RC耦合放大电路构成。根据Z1和Z2,Vo被分压为V和Vβ。若调整Z1、Z2的RC为恰当数值,则可使Vo和Vβ成为同相,实现正反馈而产生振荡。由Cf、Rf、RE1施加负反馈以期放大电路稳定化。这一电路因为稳定且频率易改变而使用于低频振荡器中。
7.6
振荡电路的稳定化7.6.1
保持振荡频率和输出电压稳定若发射机的振荡频率及输出功率发生变化,那么在接收端将发生怎样 的场面呢。这就是一会儿要调台,一会儿要调整音量,变得手不能离开收音机的原因。因此发射机的振荡频率和输出功率必须是稳定的。
不限于发射机,其它设备的频率及输出的大小也必须是恒定的。为此,对振荡电路的振荡频率和输出电压实行稳定化。
7.6.2
变化的原因有哪些?有何对策?(a)电源电压的变化
电源电压一旦变化,晶体三极管的偏置就发生变化。因为晶体三极管的参数随偏置而变化,所以输入阻抗Zi也变化,它对正反馈电路产生影响使振荡频率变化。另外,放大电路的放大倍数变化使输出电压也产生变化。
对策为由稳压电源电路提供电源,在偏置电路中使用稳压二极管以保持恒定的电压。
(b)周围温度的变化
晶体三极管地温度敏感。R、L、C的值也随温度的变化而变化。连石英晶体都受温度影响。为此,进行散热和保温。特别是为了获得高稳定度,将石英晶体放入保持恒定温度的恒温槽中。
(c)负载的变化
负载一旦改变则等效于正反馈电路的参数变化,故振荡频率及输出电压变化。
为了防止负载的影响,作为对策应尽量使得与负载电路的耦合松散且不宜取大的输出。在大输出必要的情况下,振荡电路和负载之间插入缓冲放大电路以屏蔽负载的影响。
(d)振动及冲击
振荡电路所使用的元件在振动及冲击的影响下参数发生变化。设计抗机械振动性强的结构,对设备的处理给予足够的重视。
本章小结
利用正反馈产生振荡
变压器耦合调谐式振荡
反相耦合变压器,初级端与次级端极性相反,相位差为180。![]()
LC振荡电路
由L和C对输出电压分压形成正反馈。哈特莱电路与科耳皮兹电路中的L和C对偶。![]()
使用石英晶体的晶体振荡电路
石英晶体的固有振动频率极其稳定且精度高。晶体代替L使用,获得高的Q值。![]()
RC耦合正反馈移相式
利用RC移相电路相位移动180=移相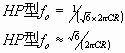
两级放大桥式
两级放大电路中,由于初级输入信号和第2级的输出信号为同相,所以输出信号相位不变即形成正反馈。![]()
振荡频率与输出电压的变化及对策
电源电压的变化→稳压电路
周围温度的变化→隔热、恒温槽、散热负载的变化→和负载松散耦合,缓冲放大电路振动·冲击→抗振动结构,竭力避免振动·冲击各种各样的振荡电路.
上一篇:由集成运算放大器构成的电路实例 2026-02-05
下一篇:数学与电路的结合 2026-02-05

 收藏本站
收藏本站
 当前位置:
当前位置:







