收藏本站
当前位置：数学与电路的结合
——逻辑数学与逻辑电路
数字电路是输入与输出为
0（例如电压低）和1（例如电压高）2种状态的电路。这种思考方法用数学来表示则是逻辑数学。也即是给予的条件（输入）与其结果（输出）的关系中只使用0或1的公式。这里所说的0或1是用来表示2种不同的状态。而不是表示数值的内容。这样，逻辑数学只有
0与1的内容，因而可以制成对应于逻辑数学式的电路（即逻辑电路）。本章，学习简单的逻辑数学和建立相应的目的的逻辑式，并学习如何对这个式子用逻辑电路来实现。
5.1
只有0和1的世界5.1.1
简单的规定逻辑数学只处理
2个状态。这里，将2个状态中的一个状态表现为0，另一个状态表现为1。因为不涉及0与1以外的状态，因而可以规定以下几点。如果
X≠1 则X=0如果
X≠0 则X=1因为只有
0与1的2个状态中的一个，可得到图5.4的规定。用身边的例子来看，不是男的就是女的，不是女的就是男的，其他不存在。以这个思考方法为基础，可以有逻辑乘（AND），逻辑和（OR），否定（NOT）这样3个新的规定。5.1.2 0
和1世界中的积（逻辑乘）图
5.2是只有0与1所进行的乘法运算，这里0，1不是数值，而是表示2个状态中的一个。但是，将这2个状态所表示的0与1作为数字来看，逻辑乘的结果与一般数学的乘法有相同的计算结果。这里，对于逻辑乘
Y=A·B，Y要成为1的状态，仅仅是A与B、即A and B均为1状态时。因此，逻辑乘也称为AND。同样Y=A·B·C时，只有A and B为1时，Y才为1。其他情况下Y=0。（如图5.5）。要得到与逻辑乘相同结果而制作的电路是在第
2章中学习过的AND电路。A与B，Y的关系与第3章中的真值表相同。5.1.3 1+1
不是2的和（逻辑和）逻辑乘情况下，用与普通的数学相同的计算方法计算，结果是一样的。但是逻辑和不能像普通数学那样计算。
1+1的情况，有以下的结果。一方是1的状态、另一方也是1的状态，这时，结果是哪一种状态呢？结论是1状态，即1+1=1。1+0
或0+1时，一方是0 的状态，只要另一方是1的状态，结果是1的状态，这样1+1也好，1+0也好，结论是1。换言之对于Y=A+B的逻辑式，只要A或B，即A or B是1时，Y=1。Y=0的结果，只有在A与B同时为0才成立。同样Y=A+B+C的情况，在A or B or C为1时，Y=1。因此，逻辑和又称OR（如图5.7）。利用符号表示逻辑和的式子如图
5.8所示。要得到与逻辑和相同结果而制作的电路是
OR电路。5.1.4
不是0，则是0的反面（否定）乘与和在普通数学中是存在的，而否定（不是）的思考方法是逻辑数学中特有的。在普通数学中，不是
4，这样的答案可以得出很多。而在只有0与1世界中（逻辑数学），答案是一定的。也即否定0就为1，否定1就为0。“不是0”用
，“不是1”用
。“不是A”用
表示。图5.9所示为否定式与符号。
5.2
使用公式简化电路5.2.1
由于是0或1，所以有以下情况逻辑数学并非处理数，而是处理只有
2个状态的数学。只不过是为了表现这样的状态，使用了0与1这2个符号。从这个意义上讲，不使用0与1，而使用第3章中用的L与H的表现方法也是同样的。这里，将不知为
0还是1的状态设为X，对它的逻辑乘与逻辑和更深入的探讨一下，如表5.1所示。确认这些公式正确与否，只要在X处代入0或1即可验证。例如，对于逻辑乘的X·
，X为0时0·
=0·1=0，X为1时，1·
=1·0=0，也即X不管是0还是1都有X·=0。同样，在X处用0或1代入，可知表5.1中所有公式是正确的。
5.2.2
或者结合在一起，或者分开在逻辑数学中，也有与普通数学一样，有时要加（
），或者将它们分开的方法。但是，必须注意的是，其内容与普通数学不同。A
交换A
·B=B·AA+B=B+A
B
结合A+
（B+C）=（A+B）+CA
·（B·C）=（A·B）·CC
分配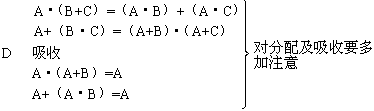
上面这些公式，有与普通数学一样的，也有完全不一样的。为了确认其正确性，只要在左右两边中，各代入
0与1的数值就可以证明。例如，在式（6）中，只要像表5.2一样，A、B、C可用0、1所有的数值代入，证明左边=右边就可以了。A、B、C的0、1组合一共有八组，将这八组数值代入时，左边均等于右边，也即式（6）得到证明。5.2.3
当公式仅为“非”时，可用AND和OR替换“非”（不是）这一种逻辑是逻辑数学的独特内容，通过使用这个否定，可以替换
AND和OR。
式（
9）和式（10）称为摩根定理。
是A与B的逻辑和的非，而 
是A的非与B的非的逻辑乘。式（9）和式（10）的证明也同样可以通过建立真值表来求得。表5.3即是为证明式（9）而做成的真值表。
5.2.4
不能除、不能减的讨论在逻辑数学中没有除法运算与减法运算，所以在
A·B=A·C时，不能两边均用A去除而得到B=C。在表5.4中，不管哪一种A·B=A·C，B均不等于C。在减法方面，例如，
，两边减去A，也不能够得到
。
5.2.5
公式变为电路，电路变为公式逻辑数学中有逻辑乘、逻辑和及否定
3种。而对应的逻辑电路有AND电路、OR电路、NOT电路3种。数学式和电路即使不同，逻辑乘与AND电路可生完全相同结果。逻辑和与OR电路，否定与NOT电路也一样。因此，即使含有多个逻辑乘、逻辑和等的公式，也必然有对应的逻辑电路存在。相反，对于含有多个AND电路和OR电路等电路时，也能求得与此对应的逻辑式（见图5.12）。（
1）探讨一下将Y=A+
的逻辑式转化成电路情况。因为这是A与B的否定的逻辑和，所以是如图5.13所示的电路。
（
2）再对稍稍复杂的公式Y=A·（
+C）求解电路。这个式中含有（ ），所以先将（ ）中的
+C变为电路，其后再求解与A的逻辑乘，其电路如图5.14所示。
（
3）不管如何复杂的、有长长的公式，均可由AND、OR、NOT这3种电路组合而成。因此，只要根据公式，按顺序地将它变为电路即可。反之，探讨如何从电路变为公式。将图
5.15(a)所示的电路变为公式时，首先考虑输入一方变为怎么样的电路（如图5.15(b)）。接着，再求后面的电路变为怎么样的公式。最终输出的公式为
Y=A·B+C·D（如图5.15(c)）。5.2.6
利用公式简化电路公式变为电路，电路变为公式都可以实现，所以在组成某电路时，首先简化公式，如果这个公式可以简化为简单式，按照简化式再组成电路，这个方法可行时，组成的电路也简单了。
例如，试组成
Y=（A+B）·（A+C）的电路。从式（6）可得A+（B·C）=（A+B）·（A+C）。利用这个公式，可以组成A+（B·C）的电路，可以得到与（A+B）·（A+C）的完全相同的结果。从图5.10可知图5.10(a)与图5.10(b)是一样的结果，比较一下，哪一种简单，是一目了然的。
5.3
各种逻辑电路5.3.1
只有全部一致时，输出才为1（一致逻辑电路）有多数的输入，如果所有的输入均为
1，输入为完全相同（一致）。当然，输入均为0，这也是一致。这种所有的输入为1或0完全一致时，才有输出为1的电路，称为一致逻辑电路（如图5.17）。这里讨论一下有
3个输入时的一致逻辑电路。因为输入有3个，其值各可取0与1，其所有组合有23=8。这8组数值的真值表可以列出，而因为输出为1的条件是只有在所有的输入为0或1才有可能，其真值表为表5.6。这样，输出要成为
1，则要A=1，B=1，C=1，所有输入一致为1时，或A=0，B=0，C=0，所有输入一致为0时。A=1
，B=1，C=1时，Y=1的逻辑式是Y=A·B·C。这是3个逻辑乘，如图5.18所示，A，B，C中只要有1个为0，Y≠1。另外，
A=0，B=0，C=0时，Y=1的逻辑式是Y=
。这是各个输入的否定（NOT）的逻辑乘，电路如图5.19所示。
这样，图
5.18和图5.19，Y均为1，所以最终电路如图5.20所示。5.3.2
表决时不用计数也可知道结果有多个输入，其中只有过半数的输入为
1时，输出为1的电路称为表决逻辑电路。这里，设有3个输入时的情况。3个输入中过半数为1有图5.21所示的4种情况。其真值表如表5.5所示（只表示输出为1的条件）。图
5.22是基于表5.5的真值表的电路情况。另外，公式可以进行简化，电路也可以简化。
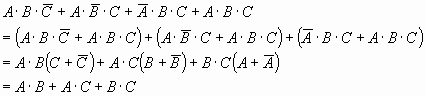
5.4
无论哪种要求都可以组成电路5.4.1
接受要求后，如何进行呢？逻辑数学是
0与1的世界。在这个局限于给出的条件为0与1、结论也是0与1的世界中，无论有什么样的要求，均可以做到。在第7章中要学习的计算机，也不过是一个根据要求，通过0与1的组合，而得到的实际电路。如图
5.24所示，如果接受到订货之后，首先是根据订货的要求建立真值表，这个工作已经在一致逻辑电路、表决逻辑电路中做过了。真值表是列出在什么样的输入时，可得到输出为1的表。接着，建立真值表的输出为
1的逻辑式。例如，输入A为1，B为0时，如果输出Y为1，那末逻辑式为Y=A·
。输出为1的情况有几种可能时，再进一步将其组合起来即可。最后再将所建立的逻辑式组成电路即大功告成。
5.4.2
要求之一……赞成限于只有一个人时举一个不是实用的例子，看一下怎样接受订货要求的。求当有几个输入时，其中只有
1个输入为1时，输出才为1的电路。这里设输入有3个时的情况。这时，赞成只限于如图5.25所示一个人，而赞成为2个人时，输出即为0。这样，有多个输入，只有其中1个为1时，输出才为1的电路，称为排他逻辑和电路。将它的输入与输出关系（条件）列出真值表如表
5.7。在表5.7中，仅仅输入A为1时，Y=1的式为Y=A·
。仅仅输入B为1时，Y=1的式为Y=
，仅仅输入C为1时，Y=1的式为Y=
·C。这3个式，无论哪一个式均是Y=1，所以整理成一个式子时，有下式
将这个式子做成电路，则如图
5.26所示。5.4.3
要求之二……专横的经理的要求因为宣称“怎么样的要求均可做到”，因此会接受到如图
5.27所示的要求。这里有经理的表现，也有职员的表现，所以会有一些难于理解的内容。用比较熟悉的形式，将经理设为
A，职员2人设为B与C，列出表5.8所示的真值表。在表
5.8的真值表中，输出Y=1的条件为A=1
，B=0，C=1A=1
，B=1，C=0A=1
，B=1，C=1中的任意一个。分别将它变成公式为
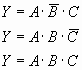
再进一步将它做成电路，则如图
5.28所示。将图
5.28的（1）＇、（2）＇、（3）＇整理成一个式子时，为Y=
将上式换成图
5.29所示的电路，就可得到照订货那样的电路了。5.4.4
小结下面，包括没有举到的例子，列出各种逻辑电路的真值表。
5.5
进行加法运算的电路（加法器）5.5.1
一半的加法器（半加器）进行
2个数的加法，如图5.31所示，第1位的加法做9+4就可以。但是第2位则不仅要做8+6，而且当第1位有进位时，还要加上这个进位。2进制的加法也与此相同。不考虑进位的加法器称为半加器(half adder)，而同时考虑进位的加法器称为全加器(full adder)。不考虑进位也即最低位的加法只有图
5.32所示的4种情况。虽然不考虑进位，作为加法的结果，在1+1时，出现向上位的进位。这里，必须注意的是，逻辑和的1+1与加法的1+1在意义上是不同的。加法是普通的数学。图
5.32中A、B和C、S的关系用别的书写方法整理一下，有表5.10一样的真值表。在表
5.10中，首先注意S。看一下A、B与S的关系。只有A、B中的任意1个为0，另1个为1时，S为1。也即只有不一致，S为1。这是前面所学习到的排他逻辑和（多数输入时，仅仅只有1个输入为1时，输出为），
·B=1或A·
=1时，S=1所以，整理成一个式子时为
S=
下面，注意一下
C，A、B两个均为1时，C=1。这是逻辑乘。因此C的式子如下C=A
·B上面的
2个逻辑式变为电路时，就可以得到如图5.33所示的半加器电路。5.5.2 2
个半加器则为1个加法器（全加器）能够进行计算从下位产生的进位的加法器为全加器，这是用
2个半加器，组成如图5.34所示电路。这样，位数即使再多，对于其中任意
1位的加法，包含有低位来的进位即可组成全加器。全加器的真值表在表5.11中列出。5.5.3
多位数的加法1
个全加器可以进行2进制数的加法运算，所以如果做2位的加法，使用2个全加器即可，具体的结构如图5.35所示。另外，最低位的
AO+BO不用考虑从下位的进位，所以用半加器即可。图
5.36所示是2进制数4位加法器IC的外观图的内部的连接图。5.5.4
减法运算用加法运算来进行计算机除了加法还做其他各种运算，而其计算的基础是加法器。乘法运算是用多次重复的加法运算，除法用多次减法运算来进行。这里试用加法运算的方法进行减法运算。
首先，将减数的
1和0取它的反，再进行加法运算（如图5.37）。加法的结果，如果最高位有进位时，将这个进位再加到其结果的最低位上，这就是答案（如图
5.38）。最高位没有进位时，答案是负（或
0），图5.39中，如上所述的方法进行时，最高位没有进位。这时，将这个加法运算的结果的1与0再一次取反，最后加上一（负）就是答案。而取1与0的反，只要使用NOT电路即可。
5.6
运算电路的实验5.6.1
做1+1=1（逻辑运算）如表
5.12所示设定各个开关时，可以进行各位的逻辑运算。例如，M=1，S3=1，S2=1，S1=1，S0=0，则YO=AO+BO，Y1=A1+B1，…。表中的Y=A+B，是表示A与B不一致时，Y为1，被称为“同门”的逻辑运算。5.6.2
做1+1=10（数值运算）2
进制4位数值运算时，如表5.13所示来设定。PLUS是“+”，MINUS是“-”，因为与逻辑运算的表示方法易混淆，所以这样来表示。另外，在减法运算时，A的高位数值第五位被设定为1
